What Is The Rate Of Change Of
Learning Outcomes
- Notice the average charge per unit of change of a part.
Gasoline costs have experienced some wild fluctuations over the last several decades. The tabular array beneath[ane] lists the average cost, in dollars, of a gallon of gasoline for the years 2005–2012. The cost of gasoline tin can be considered as a role of yr.
| [latex]y[/latex] | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| [latex]C\left(y\correct)[/latex] | 2.31 | 2.62 | 2.84 | 3.thirty | 2.41 | 2.84 | three.58 | 3.68 |
If we were interested only in how the gasoline prices changed between 2005 and 2012, we could compute that the cost per gallon had increased from $ii.31 to $3.68, an increment of $1.37. While this is interesting, it might exist more useful to look at how much the toll changed per year. In this section, nosotros volition investigate changes such every bit these.
The cost change per year is a charge per unit of change because it describes how an output quantity changes relative to the change in the input quantity. We can meet that the price of gasoline in the table above did not change past the same amount each year, so the rate of change was not constant. If we use merely the kickoff and ending data, we would be finding the average rate of change over the specified period of time. To find the average charge per unit of modify, we divide the change in the output value by the change in the input value.
[latex]\begin{align}\text{Boilerplate charge per unit of alter} &=\frac{\text{Alter in output}}{\text{Modify in input}}\\[2mm] &=\frac{\Delta y}{\Delta x}\\[2mm] &=\frac{{y}_{2}-{y}_{1}}{{ten}_{2}-{x}_{one}}\\[2mm] &=\frac{f\left({x}_{two}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}\end{align}[/latex]
The Greek letter of the alphabet [latex]\Delta [/latex] (delta) signifies the modify in a quantity; nosotros read the ratio as "delta-[latex]y[/latex] over delta-[latex]ten[/latex]" or "the change in [latex]y[/latex] divided by the change in [latex]x[/latex]." Occasionally we write [latex]\Delta f[/latex] instead of [latex]\Delta y[/latex], which nevertheless represents the change in the function'due south output value resulting from a modify to its input value.
In our instance, the gasoline price increased by $1.37 from 2005 to 2012. Over 7 years, the average charge per unit of change was
[latex]\dfrac{\Delta y}{\Delta 10}=\dfrac{{one.37}}{\text{7 years}}\approx 0.196\text{ dollars per year}[/latex]
On boilerplate, the price of gas increased by well-nigh 19.6¢ each twelvemonth.
Other examples of rates of change include:
- A population of rats increasing by 40 rats per calendar week
- A auto traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes)
- A automobile driving 27 miles per gallon of gasoline (altitude traveled changes by 27 miles for each gallon)
- The current through an electrical excursion increasing by 0.125 amperes for every volt of increased voltage
- The amount of money in a college account decreasing by $four,000 per quarter
A General Note: Rate of Change
A rate of modify describes how an output quantity changes relative to the change in the input quantity. The units on a rate of change are "output units per input units."
The average charge per unit of alter betwixt ii input values is the full change of the function values (output values) divided by the modify in the input values.
[latex]\dfrac{\Delta y}{\Delta x}=\dfrac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{two}-{ten}_{one}}[/latex]
How To: Given the value of a function at different points, calculate the boilerplate rate of change of a function for the interval between two values [latex]{x}_{1}[/latex] and [latex]{x}_{two}[/latex].
- Calculate the deviation [latex]{y}_{2}-{y}_{i}=\Delta y[/latex].
- Calculate the deviation [latex]{x}_{2}-{x}_{1}=\Delta 10[/latex].
- Find the ratio [latex]\dfrac{\Delta y}{\Delta x}[/latex].
Example: Computing an Boilerplate Rate of Modify
Using the data in the table beneath, find the average charge per unit of modify of the price of gasoline betwixt 2007 and 2009.
| [latex]y[/latex] | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| [latex]C\left(y\correct)[/latex] | 2.31 | ii.62 | ii.84 | 3.30 | ii.41 | 2.84 | 3.58 | 3.68 |
The following video provides some other example of how to observe the average rate of alter betwixt two points from a table of values.
Endeavor It
Using the information in the tabular array below, find the average rate of change betwixt 2005 and 2010.
| [latex]y[/latex] | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| [latex]C\left(y\correct)[/latex] | 2.31 | 2.62 | 2.84 | 3.thirty | 2.41 | two.84 | three.58 | 3.68 |
Testify Solution
[latex]\dfrac{$2.84-$2.31}{5\text{ years}}=\dfrac{$0.53}{v\text{ years}}=$0.106[/latex] per year.
Case: Calculating Average Rate of Change from a Table
After picking upwardly a friend who lives 10 miles away, Anna records her distance from home over time. The values are shown in the table beneath. Detect her average speed over the start six hours.
| t (hours) | 0 | 1 | ii | 3 | 4 | 5 | six | 7 |
| D(t) (miles) | 10 | 55 | ninety | 153 | 214 | 240 | 282 | 300 |
Example: Computing Average Rate of Modify from a Graph
Given the function [latex]g\left(t\correct)[/latex], find the average charge per unit of change on the interval [latex]\left[-1,2\right][/latex].
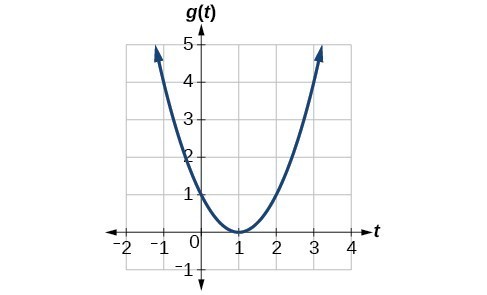
Example: Computing Average Rate of Change for a Function Expressed as a Formula
Compute the average rate of change of [latex]f\left(x\right)={ten}^{two}-\frac{1}{10}[/latex] on the interval [latex]\text{[2,}\text{four].}[/latex]
The post-obit video provides another instance of finding the average charge per unit of change of a function given a formula and an interval.
Endeavour It
Find the average rate of change of [latex]f\left(x\right)=ten - 2\sqrt{x}[/latex] on the interval [latex]\left[i,9\correct][/latex].
Show Solution
[latex]\dfrac{1}{2}[/latex]
Example: Finding the Boilerplate Rate of Change of a Strength
The electrostatic force [latex]F[/latex], measured in newtons, between two charged particles tin exist related to the altitude between the particles [latex]d[/latex], in centimeters, by the formula [latex]F\left(d\right)=\frac{two}{{d}^{two}}[/latex]. Find the average rate of change of forcefulness if the altitude between the particles is increased from ii cm to 6 cm.
Instance: Finding an Average Rate of Change equally an Expression
Find the boilerplate rate of change of [latex]chiliad\left(t\correct)={t}^{2}+3t+1[/latex] on the interval [latex]\left[0,a\right][/latex]. The answer will be an expression involving [latex]a[/latex].
Effort Information technology
Find the boilerplate charge per unit of alter of [latex]f\left(ten\right)={x}^{two}+2x - viii[/latex] on the interval [latex]\left[5,a\correct][/latex].
Show Solution
[latex]a+seven[/latex]
Contribute!
Did you have an idea for improving this content? We'd love your input.
Improve this pageLearn More
Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/rates-of-change-and-behaviors-of-graphs/
Posted by: georgewrond1958.blogspot.com

0 Response to "What Is The Rate Of Change Of"
Post a Comment